Metadata
aliases: []
shorthands: {}
created: 2021-11-02 19:05:02
modified: 2022-06-24 00:16:24
The spring model of lattice vibrations is a further simplification from the harmonic approximation of lattice vibrations that we can use to model the thermal motion of atoms in a crystal.
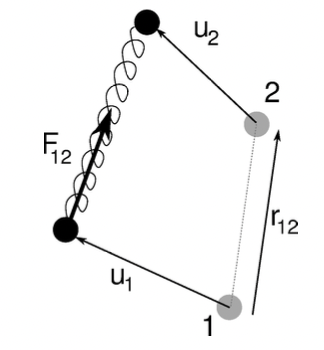
In the harmonic approximation, we noted that the forces acting on the atoms depend linearly on their relative position from the equilibrium state, so the interaction of the atoms can be modeled like they are connected with springs. In this case every atom would be connected to every other atom, but in this model we simplify this case by only considering the strongest ones of the springs (first and second neighbors).

Let us consider the general formula for the force between two arbitrary atoms:
Where
The direction:
The magnitude:
So the spring force is:
Where
There are some special cases for this: