2021-11-12 ↩

aliases: []
shorthands: {}
created: 2021-11-12 17:36:03
modified: 2022-01-10 04:47:29

Group theory homework #9

1.

Let be a group and is a fully decomposable representation. Prove that if , then every irreducible subspace of in is an invariant subspace of .

Solution

Since is fully decomposable, we can consider its irreducible representations: with the characters of these irreducible representations, . Using the characters, we can construct the projector that projects into the corresponding irreducible subspaces:

The image of a projector is the invariant subspace of , is also an invariant subspace of .

If the projector commutes with , then is an invariant subspace of it.

Commuting matrices preserve each other's invariant subspaces This means that every invariant subspace of is also an invariant subspace of . QED

2.

The representation induced by the following mechanical system:

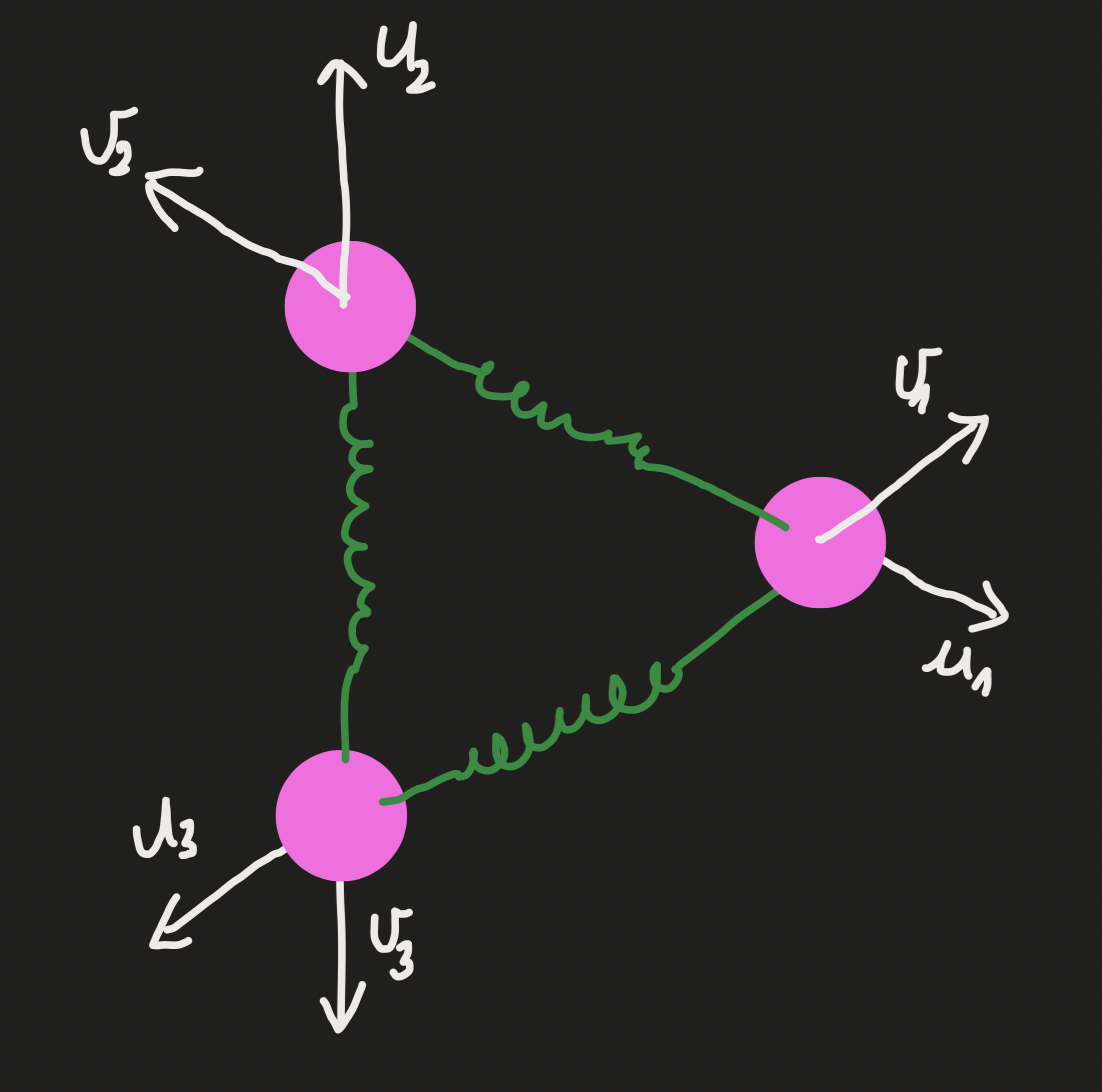
A)

The projector into :

The rank of :

Means that it has only linearly independent row or column vectors.

B)

The first four columns are linearly independent, so they can generate the image of by linear span:

C)

We have two dimensions in that represent homogeneous translation in the plane.
This is one of them, describing motion along the axis:

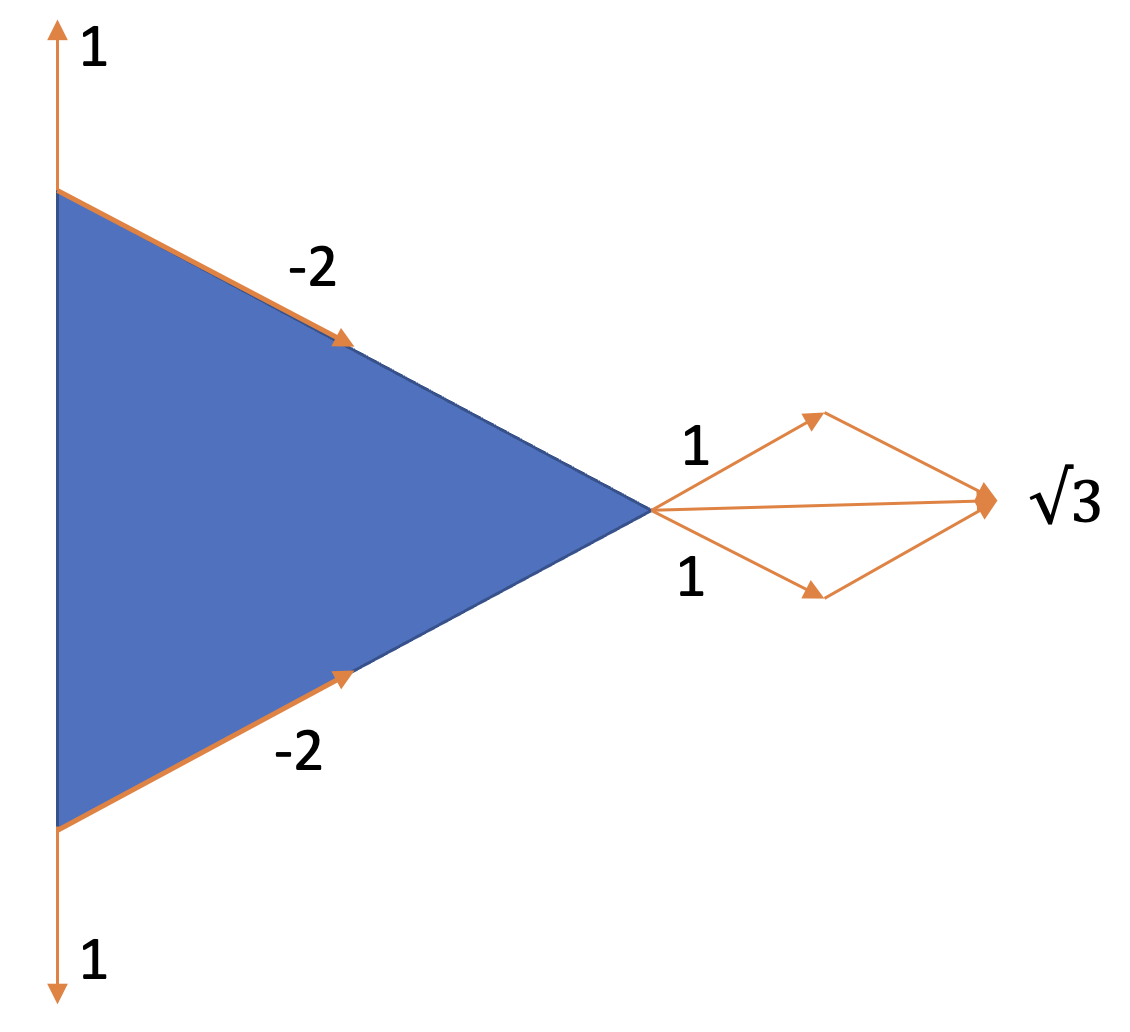
An other one can be obtained by rotating by :

These vectors are both contained within the space.