Metadata
aliases: []
shorthands: {}
created: 2022-01-10 12:09:19
modified: 2022-01-16 17:24:43
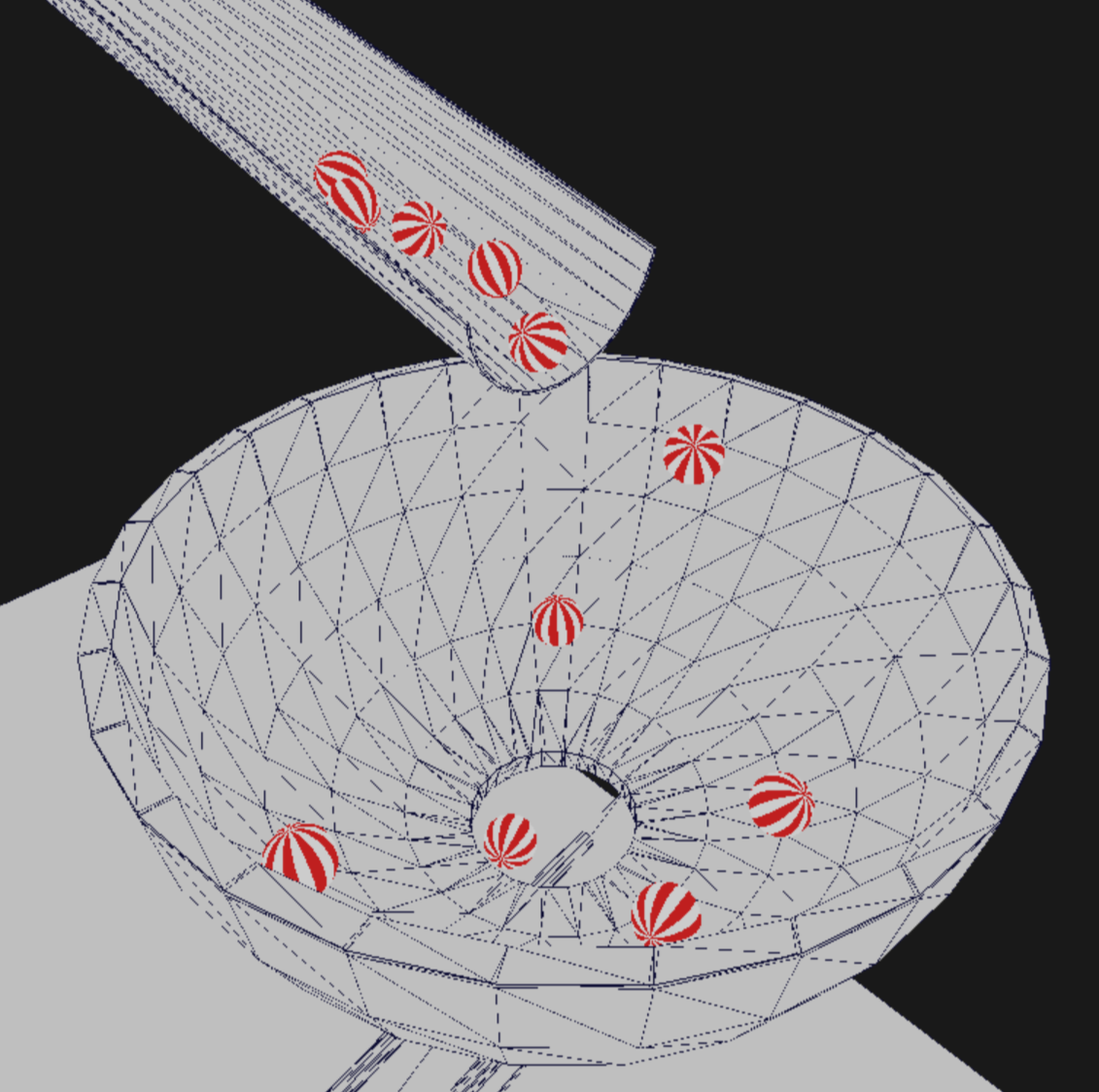
Project name: Marble Run
Project description: A 3D rigid body simulation program in which we can simulate the motion of rigid spheres in any 3D static world. Written in C++.
The source code can be viewed on GitHub, along with a version that can be run in a web browser without translation.

After opening the program, you can move the camera arbitrarily around the displayed geometry and place spheres that mimic the physics of the real world with their movement. Of course, the simulation procedure of the program is only the result of rough approximations, so it can often happen that the placed balls move along an unexpected path. Placing many balls may slow down the program, in which case you can remove the balls from the scene by pressing R, reducing the amount of lag.
Other scenes can be loaded into the program by dragging a scene file into the window then releasing it. There are some example scene files are in the scenes folder.
The program uses SDL to create the window and handle the events, and the 3D rendering is done with OpenGL ES 2. Scenes are read from files with the extension .scene. These polygon-based geometries are stored in the same way as in Wavefront .obj files, but they also look for lines beginning with #ball… at the beginning of the files, which may describe the position and properties of the balls already present in the scene.
This class represents 3-dimensional vectors whose coordinates are interpreted in the standard Cartesian coordinate system, and the associated functions implement operations that can be performed on vectors. The coordinates are stored in 32-bit floats to make them compatible with OpenGL. The declaration and implementation of the class are contained in the Vec3.h and Vec3.cpp files. The data members x,y, z are public in this class.
```c++
class Vec3{…};
### Constructor
Creates the vector with the coordinates obtained as arguments.
c++
Vec3(float x_ = 0, float y_ = 0, float z_ = 0): x (x), y (y), z (z_) {}
### Vector length
The `len` member function returns the length of the vector, and the `lenSq` function returns the square of its length. Getting the square is much faster, as there is no need to calculate the square root. This implements the <a href="Euclidean space.html#norm" title="Euclidean space#Norm">Euclidean norm</a>.
c++
float len() const;
float lenSq() const;
### Setting length
The `setLen` function allows you to set the length of the vector to a new value while maintaining its direction. You can also normalize the vector with this function: `v.setLen(1.0f)`.
c++
Vec3 & setLen(float newLen);
### Multiplication, division by scalar
The `mult` and `div` functions can be used to multiply or divide a vector by a scalar value.
c++
Vec3 & mult(float val);
Vec3 & div(float val);
### Adding and subtracting another vector
Use the `add` and `sub` functions to add or subtract another vector from our vector.
c++
Vec3 & add(const Vec3 & other);
Vec3 & sub(const Vec3 & other);
### Rotation
The vector can be rotated around the axes of the coordinate system. The angle must be specified in radians.
c++
Vec3 & rotateX(float angle);
Vec3 & rotateY(float angle);
Vec3 & rotateZ(float angle);
### Apply any <a href="Matrix.html" title="matrix">matrix</a> transformation
A transformation stored in any <mjx-container class="MathJax" jax="SVG"><svg style="vertical-align: 0;" xmlns="http://www.w3.org/2000/svg" width="5.028ex" height="1.532ex" role="img" focusable="false" viewBox="0 -677 2222.4 677" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-3518-TEX-N-34" d="M462 0Q444 3 333 3Q217 3 199 0H190V46H221Q241 46 248 46T265 48T279 53T286 61Q287 63 287 115V165H28V211L179 442Q332 674 334 675Q336 677 355 677H373L379 671V211H471V165H379V114Q379 73 379 66T385 54Q393 47 442 46H471V0H462ZM293 211V545L74 212L183 211H293Z"></path><path id="MJX-3518-TEX-N-D7" d="M630 29Q630 9 609 9Q604 9 587 25T493 118L389 222L284 117Q178 13 175 11Q171 9 168 9Q160 9 154 15T147 29Q147 36 161 51T255 146L359 250L255 354Q174 435 161 449T147 471Q147 480 153 485T168 490Q173 490 175 489Q178 487 284 383L389 278L493 382Q570 459 587 475T609 491Q630 491 630 471Q630 464 620 453T522 355L418 250L522 145Q606 61 618 48T630 29Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mn"><use data-c="34" xlink:href="#MJX-3518-TEX-N-34"></use></g><g data-mml-node="mo" transform="translate(722.2,0)"><use data-c="D7" xlink:href="#MJX-3518-TEX-N-D7"></use></g><g data-mml-node="mn" transform="translate(1722.4,0)"><use data-c="34" xlink:href="#MJX-3518-TEX-N-34"></use></g></g></g></svg></mjx-container> matrix can be applied to the vector.
c++
Vec3 & applyMatrix(const Matrix & matrix);
These functions return references to the original vector so the operations can be chained like this:
c++
v.rotateX(1.57f).mult(2.5f).add(otherVector);
### Cross product
<a href="Cross product.html" title="Cross product">Vector product</a> can be performed on two vectors. Two functions allow this, one is static, but both do the same: return the resulting vector and do not change any of the input vectors.
c++
Vec3 cross(const Vec3 & other) const;
static Vec3 cross(const Vec3 & v1, const Vec3 & v2);
### Dot product
We also have two functions to perform a <a href="Dot product.html" title="Dot product">dot product</a>.
c++
float dot(const Vec3 & o) const;
static float dot(const Vec3 & v1, const Vec3 & v2);
### Static addition, subtraction, scalar multiplication
Static functions can be used to add, subtract, and multiply by scalars. These functions do not change the value of the vector(s) involved, but give the result as a return value.
c++
static Vec3 add(const Vec3 & v1, const Vec3 & v2);
static Vec3 sub(const Vec3 & v1, const Vec3 & v2);
static Vec3 mult(const Vec3 & v1, float a);
### <a href="Dot product.html#fb28d6" title="dot product#^fb28d6">angle between two vectors</a>
The angle between two vectors can be obtained with a static function. The return value is the angle in radians.
c++
static float angle(const Vec3 & v1, const Vec3 & v2);
### Overloaded operators
Some of the listed operations can be performed with overloaded operators.
## <mjx-container class="MathJax" jax="SVG"><svg style="vertical-align: 0;" xmlns="http://www.w3.org/2000/svg" width="5.028ex" height="1.532ex" role="img" focusable="false" viewBox="0 -677 2222.4 677" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-3519-TEX-N-34" d="M462 0Q444 3 333 3Q217 3 199 0H190V46H221Q241 46 248 46T265 48T279 53T286 61Q287 63 287 115V165H28V211L179 442Q332 674 334 675Q336 677 355 677H373L379 671V211H471V165H379V114Q379 73 379 66T385 54Q393 47 442 46H471V0H462ZM293 211V545L74 212L183 211H293Z"></path><path id="MJX-3519-TEX-N-D7" d="M630 29Q630 9 609 9Q604 9 587 25T493 118L389 222L284 117Q178 13 175 11Q171 9 168 9Q160 9 154 15T147 29Q147 36 161 51T255 146L359 250L255 354Q174 435 161 449T147 471Q147 480 153 485T168 490Q173 490 175 489Q178 487 284 383L389 278L493 382Q570 459 587 475T609 491Q630 491 630 471Q630 464 620 453T522 355L418 250L522 145Q606 61 618 48T630 29Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mn"><use data-c="34" xlink:href="#MJX-3519-TEX-N-34"></use></g><g data-mml-node="mo" transform="translate(722.2,0)"><use data-c="D7" xlink:href="#MJX-3519-TEX-N-D7"></use></g><g data-mml-node="mn" transform="translate(1722.4,0)"><use data-c="34" xlink:href="#MJX-3519-TEX-N-34"></use></g></g></g></svg></mjx-container> matrix class
This class describes <mjx-container class="MathJax" jax="SVG"><svg style="vertical-align: 0;" xmlns="http://www.w3.org/2000/svg" width="5.028ex" height="1.532ex" role="img" focusable="false" viewBox="0 -677 2222.4 677" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-3520-TEX-N-34" d="M462 0Q444 3 333 3Q217 3 199 0H190V46H221Q241 46 248 46T265 48T279 53T286 61Q287 63 287 115V165H28V211L179 442Q332 674 334 675Q336 677 355 677H373L379 671V211H471V165H379V114Q379 73 379 66T385 54Q393 47 442 46H471V0H462ZM293 211V545L74 212L183 211H293Z"></path><path id="MJX-3520-TEX-N-D7" d="M630 29Q630 9 609 9Q604 9 587 25T493 118L389 222L284 117Q178 13 175 11Q171 9 168 9Q160 9 154 15T147 29Q147 36 161 51T255 146L359 250L255 354Q174 435 161 449T147 471Q147 480 153 485T168 490Q173 490 175 489Q178 487 284 383L389 278L493 382Q570 459 587 475T609 491Q630 491 630 471Q630 464 620 453T522 355L418 250L522 145Q606 61 618 48T630 29Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mn"><use data-c="34" xlink:href="#MJX-3520-TEX-N-34"></use></g><g data-mml-node="mo" transform="translate(722.2,0)"><use data-c="D7" xlink:href="#MJX-3520-TEX-N-D7"></use></g><g data-mml-node="mn" transform="translate(1722.4,0)"><use data-c="34" xlink:href="#MJX-3520-TEX-N-34"></use></g></g></g></svg></mjx-container> <a href="Matrix.html" title="Matrix">matrices</a> in which we can store <a href="Linear map.html" title="Linear map">linear transformations</a>. The declaration and implementation of the class are contained in the files `Matrix.h` and `Matrix.cpp`.
c++
class Matrix{…};
### Constructor
The constructor does not get any arguments and creates a <mjx-container class="MathJax" jax="SVG"><svg style="vertical-align: 0;" xmlns="http://www.w3.org/2000/svg" width="5.028ex" height="1.532ex" role="img" focusable="false" viewBox="0 -677 2222.4 677" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-3521-TEX-N-34" d="M462 0Q444 3 333 3Q217 3 199 0H190V46H221Q241 46 248 46T265 48T279 53T286 61Q287 63 287 115V165H28V211L179 442Q332 674 334 675Q336 677 355 677H373L379 671V211H471V165H379V114Q379 73 379 66T385 54Q393 47 442 46H471V0H462ZM293 211V545L74 212L183 211H293Z"></path><path id="MJX-3521-TEX-N-D7" d="M630 29Q630 9 609 9Q604 9 587 25T493 118L389 222L284 117Q178 13 175 11Q171 9 168 9Q160 9 154 15T147 29Q147 36 161 51T255 146L359 250L255 354Q174 435 161 449T147 471Q147 480 153 485T168 490Q173 490 175 489Q178 487 284 383L389 278L493 382Q570 459 587 475T609 491Q630 491 630 471Q630 464 620 453T522 355L418 250L522 145Q606 61 618 48T630 29Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mn"><use data-c="34" xlink:href="#MJX-3521-TEX-N-34"></use></g><g data-mml-node="mo" transform="translate(722.2,0)"><use data-c="D7" xlink:href="#MJX-3521-TEX-N-D7"></use></g><g data-mml-node="mn" transform="translate(1722.4,0)"><use data-c="34" xlink:href="#MJX-3521-TEX-N-34"></use></g></g></g></svg></mjx-container> identity matrix.
c++
Matrix();
### Matrix multiplication
Two matrices can be multiplied by standard <a href="Matrix multiplication.html" title="Matrix multiplication">matrix multiplication</a>, combining the two transformations.
c++
void mult(const Matrix & other);
static Matrix mult(const Matrix & a, const Matrix & b);
The static function does not change any of the matrices, but the return value is the result. The non-static member function changes the matrix on which we call it.
The two operations can also be performed with operators:
c++
Matrix & operator=(const Matrix & other);
Matrix operator(const Matrix & other) const; // Corresponds to static function
### Multiplication by scalar
The matrix can be multiplied by a scalar value with overloaded operators.
c++
Matrix & operator=(const float scalar);
Matrix operator(const float scalar) const;
### Left multiplication
In many cases, you need to multiply from the left to successfully combine two transformations. This is done by the `applyTransformation` member function.
c++
void applyTransformation (const Matrix & t);
### Static functions for implementing frequent transformations
The static functions listed below can be used to create matrices that perform frequently required transformations, for example <a href="Rotation matrix.html" title="Rotation matrix">rotations</a>. All angles must be specified in radians.
c++
// Scaling by the same coefficient in all directions
static Matrix scaling(float factor);
// Scaling to different degrees in different directions
static Matrix scaling(float factorX, float factorY, float factorZ);
// Offset (spatial translation)
static Matrix translation(float x, float y, float z);
// Rotate around the X axis
static Matrix rotationX(float angle);
// Rotate around the Y axis
static Matrix rotationY(float angle);
// Rotate around the Z axis
static Matrix rotationZ(float angle);
// Rotate around any axis (axis must be a unit vector)
static Matrix rotation(float angle, float ux, float uy, float uz);
// Rectangular slice transformation: transforms a truncated pyramid space of a given size into a cube, the basis of the transformation of the perspective representation is given
static Matrix frustum(float left, float right, float bottom, float top, float zNear, float zFar);
// Perspective transformation
static Matrix perspective(float fov, float aspectRatio, float zNear, float zFar);
In the implementation of the `perspective` and `frustum` transformations, the [ARM Developer Center](https://arm-software.github.io/opengl-es-sdk-for-android/simple_cube.html) helped as a reference.
### Pointer to the elements of the matrix
The `getElements` member function provides the pointer to the array of elements of the matrix. This is needed when passing it to the OpenGL shader e.g. the camera matrix before rendering.
c++
const float * getElements() const;
## Shaders
The shaders used in the program are contained in the `Shaders.h` and `Shaders.cpp` files.
### The vertex shader
The program uses a very simple vertex shader. This shader transforms the points in the scene into screen space with the perspective view of the camera and the model view matrix of the model is applied as well. Interestingly, the <mjx-container class="MathJax" jax="SVG"><svg style="vertical-align: -0.025ex;" xmlns="http://www.w3.org/2000/svg" width="1.294ex" height="1.025ex" role="img" focusable="false" viewBox="0 -442 572 453" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-3522-TEX-I-1D465" d="M52 289Q59 331 106 386T222 442Q257 442 286 424T329 379Q371 442 430 442Q467 442 494 420T522 361Q522 332 508 314T481 292T458 288Q439 288 427 299T415 328Q415 374 465 391Q454 404 425 404Q412 404 406 402Q368 386 350 336Q290 115 290 78Q290 50 306 38T341 26Q378 26 414 59T463 140Q466 150 469 151T485 153H489Q504 153 504 145Q504 144 502 134Q486 77 440 33T333 -11Q263 -11 227 52Q186 -10 133 -10H127Q78 -10 57 16T35 71Q35 103 54 123T99 143Q142 143 142 101Q142 81 130 66T107 46T94 41L91 40Q91 39 97 36T113 29T132 26Q168 26 194 71Q203 87 217 139T245 247T261 313Q266 340 266 352Q266 380 251 392T217 404Q177 404 142 372T93 290Q91 281 88 280T72 278H58Q52 284 52 289Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mi"><use data-c="1D465" xlink:href="#MJX-3522-TEX-I-1D465"></use></g></g></g></svg></mjx-container> and <mjx-container class="MathJax" jax="SVG"><svg style="vertical-align: -0.464ex;" xmlns="http://www.w3.org/2000/svg" width="1.109ex" height="1.464ex" role="img" focusable="false" viewBox="0 -442 490 647" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-3523-TEX-I-1D466" d="M21 287Q21 301 36 335T84 406T158 442Q199 442 224 419T250 355Q248 336 247 334Q247 331 231 288T198 191T182 105Q182 62 196 45T238 27Q261 27 281 38T312 61T339 94Q339 95 344 114T358 173T377 247Q415 397 419 404Q432 431 462 431Q475 431 483 424T494 412T496 403Q496 390 447 193T391 -23Q363 -106 294 -155T156 -205Q111 -205 77 -183T43 -117Q43 -95 50 -80T69 -58T89 -48T106 -45Q150 -45 150 -87Q150 -107 138 -122T115 -142T102 -147L99 -148Q101 -153 118 -160T152 -167H160Q177 -167 186 -165Q219 -156 247 -127T290 -65T313 -9T321 21L315 17Q309 13 296 6T270 -6Q250 -11 231 -11Q185 -11 150 11T104 82Q103 89 103 113Q103 170 138 262T173 379Q173 380 173 381Q173 390 173 393T169 400T158 404H154Q131 404 112 385T82 344T65 302T57 280Q55 278 41 278H27Q21 284 21 287Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mi"><use data-c="1D466" xlink:href="#MJX-3523-TEX-I-1D466"></use></g></g></g></svg></mjx-container> coordinates of the output vector had to be multiplied by a factor. If the shader did not do this, the image at the edge of the screen would be greatly distorted. I don’t know if this is a standard procedure, but the point is, it works.
c++
const GLchar* Shaders::baseVertex;
### The pixel shader
The pixel (fragment) shader is very simple: it only gives the point a predefined color. Because the geometry behind the camera was also drawn for some reason (in principle, the system should have clipped it on its own, but it didn't), the shader colors the pixels behind the camera to be transparent.
c++
const GLchar* Shaders::customColorFragment;
## Camera class
This class allows you to easily manage your camera to be compatible with OpenGL. The declaration and implementation of the class are contained in the `Camera.h` and `Camera.cpp` files.
c++
class Camera{…};
### Constructor
It creates the camera, places it in the origin, and sets a base direction, angle of view, and aspect ratio of it.
c++
Camera();
### Position getter and setter
The position of the camera can be queried with a getter, which returns it as a vector. The position setter can be used to adjust your position.
c++
Vec3 getPos() const;
void setPos(const Vec3 & newPos);
### Shifting the camera position
The camera can be shifted from its current position with the `moveBy` member function.
c++
void moveBy (const Vec3 & d);
### Set and query viewing direction
Another important feature of the camera besides its position is where it looks. This can be set with a direction vector and the direction can be queried at any time with the getter.
c++
void setDir(const Vec3 & newDir);
Vec3 getDir() const;
### Setting a target
Another way to align the camera is to specify the point where you want the camera to look at it. This point can be specified as a vector.
c++
void lookAt(const Vec3 & target);
### Adjust the aspect ratio
Another important feature of the camera is the aspect ratio. To create this perspective matrix, the objects on the display must not be distorted. This can be set with the `setAspectRatio` setter. This ratio is good if it matches the aspect ratio of the window.
c++
void setAspectRatio(float newAr);
### Adjusting the field of view
The field of view determines the viewing angle at which the geometry will be displayed by the camera. At a larger angle, more will be visible, but the edge of the image will be more distorted. This can be set with the `setFOV` setter. The angle must be specified in radians.
c++
void setFOV(float newFov);
### Rotate the camera left and right
The camera can be rotated to the right or left by an angle specified in radians. The rotation is about an axis parallel to the upward direction.
c++
void turnRight(float angle);
void turnLeft(float angle);
### Tilting the camera down or up
The viewing direction of the camera can be tilted up or down with the `tiltUp` member function. The angle must be specified in radians. You can tilt the camera down with a negative angle. The function ensures that you do not tilt the camera too much.
c++
void tiltUp(float angle);
### Query the relative right direction
The `getRightDir` member function returns the relative horizontal direction of the camera to the right as a vector. The returned vector is of unit length.
c++
Vec3 getRightDir() const;
### Querying the relative forward direction
The relative forward, horizontal direction of the camera can also be queried using the `getForwardDir` member function. The returned vector is of unit length. This value is useful when moving the camera horizontally forward.
c++
Vec3 getForwardDir() const;
### Generate a projection matrix
A perspective projection matrix generated from the properties of the camera can also be queried. The matrix obtained as the return value is compatible with OpenGL. Clipping distances must be specified as arguments. These are the distances between the objects that will be displayed.
c++
Matrix getProjMatrix(float zNear, float zFar) const;
## 3d model class
A class that represents 3D models. It also stores the geometry of the model in CPU memory and in GPU memory through the OpenGL API. It stores the coordinates of the vertices that make up the model and the indices of the triangles in a separate dynamic array. The declaration and implementation of the class are contained in the `Model.h` and `Model.cpp` files.
c++
class Model{…};
### Constructor, destructor
The class constructor registers the vertex buffer and the element buffer through OpenGL, in which the geometry of the model will be stored in GPU memory. It also initially resets arrays containing vertices and indices.
c++
Model();
~Model();
### Loading geometric data into cpu memory
The `loadModel` virtual (that is, it can be overridden by subclasses) member function loads the geometry data to be stored into dynamic arrays. By default, it loads only a simple octahedron in this primitive class.
c++
virtual void loadModel();
### Loading data into gpu memory
The `loadToGL` member function loads the previously loaded/generated geometry into the registered buffers. In case of multiple invocations, the previously allocated GPU memory will be freed before reloading.
c++
void loadToGL() const;
### Binding buffers
Buffers must be bound before rendering. Once this is done, the called OpenGL drawing function will draw based on the most recently bound data. It is not advisable to use this function externally, except when implementing custom rendering.
c++
void bindBuffers() const;
### Drawing
The rendering of the model can be done by calling the `render` function. The function must pass the vertex attribute pointer used. This describes to OpenGL the format in which we pass the vertices to it (so how many dimensions there are, if we want to use UV coordinates and normal ones, it should be more than 3 dimensions). You also need to tell it which rendering method to use. This is normal raster rendering by default, but could be set to e.g. polyline.
c++
void render(GLint posAttrib, GLenum mode = GL_TRIANGLES) const;
### Draw by triangle
The rendering can be run one at a time, dividing the model into triangles. This can be useful if you want to draw a wireframe in polyline mode. It is important to note that this way to draw much slower.
c++
void renderOneByOne(GLint posAttrib, GLenum mode = GL_TRIANGLES) const;
### Querying the model vertex number
The `getVertexNum` function returns how many vertices make up the model.
c++
GLuint getVertexNum() const;
### Querying one of the vertices of the model
One of the vertices of the model can be queried by specifying its index. The function returns this as a 3D vector.
c++
Vec3 getVertex(GLuint index) const;
### Querying the number of triangles
The `getTriangleNum` member function returns how many triangles make up the model.
c++
GLuint getTriangleNum() const;
### Querying a triangle
You can also query the corner points of a given triangle with the `getTriangle` member function. The function has no return value, but sets the vectors equal to the corresponding corner points through the three vector pointers passed in the argument. Of course, the index of the triangle to be queried must also be given.
c++
void getTriangle(GLuint index, Vec3 * a, Vec3 * b, Vec3 * c) const;
### Query the indices of a triangle's vertices
As with the previous member function, the vertex numbers of the given triangle can be queried if we are only interested.
c++
void getTriangleIdx(GLuint index, GLuint * a, GLuint * b, GLuint * c) const;
## Model loaded from a file
A subclass derived from the `Model` class is `ObjModel`, which can load the geometry from a file by giving it the filename. You can load Wavefront .obj files, but not all of them work. It is guaranteed to work with the files in the scenes folder, they only have the syntax they can handle. The class declaration and implementation are contained in the `ObjModel.h` and `ObjModel.cpp` files.
c++
class ObjModel: public Model{…};
### Constructor
The constructor does the same thing as the parent class, we can just give it a filename from which it will read the data.
c++
ObjModel(const char * fileName_ = ""): Model(), fileName(fileName_) {};
The filename can be changed later before calling `loadModel`.
c++
void setFileName(const char * name);
### Load model
The subclass overrides the `loadModel` virtual function of the parent class, in which it loads the geometry from the specified file.
c++
void loadModel() override;
### Load geometry from input stream
`LoadModel` also uses this overloaded operator. It reads from the input stream line by line and reads the file that way.
c++
friend std::istream& operator>>(std::istream& is, ObjModel& model);
## Sphere model
A subclass derived from the `Model` class is `SphereModel`, which generates a sphere with the specified parameters, which can then be rendered this way. The class declaration and implementation are contained in the `SphereModel.h` and `SphereModel.cpp` files.
c++
class SphereModel: public Model{…};
### Constructor
We can tell the constructor of the subclass the resolution and the radius of the sphere we want the `loadModel` function to generate for us. Resolution is the number of steps you take to make points on a sphere. The higher the resolution, the smoother the surface of the sphere, but the longer it takes to draw.
c++
SphereModel(int resolution = 12, float radius = 1.0f);
### Generating the sphere
The sphere geometry is generated by the overridden `loadModel` virtual member function according to the specified parameters.
c++
void loadModel() override;
### Get and set radius and resolution
You can change the radius and resolution of the sphere with setters and getters after initialization, but before calling `loadModel`.
c++
void setResolution(int newRes);
void setRadius(float r);
int getResolution() const;
float getRadius() const;
### Striped rendering
The sphere can be drawn in stripes with the `renderStriped` member function. The boolean value that can be specified for the function determines whether the program draws even or odd stripes. With this function, you can see the look reminiscent of a beach ball seen in the program.
c++
void renderStriped(GLint posAttrib, bool side = false) const;
## Ball class
The `Ball` class describes the balls that appear in the program and the actions that can be performed on them. The declaration and implementation of the class are contained in the `Ball.h` and `Ball.cpp` files.
c++
class Ball{…};
### Constructor
You can specify the initial position and radius of the ball for the constructor. Sets the other properties as default. (zero velocity, zero angular velocity, one density, …)
c++
Ball(const Vec3 & pos_ = Vec3 (0, 0, 0), float radius = 1);
### Density
The ball has a density based on which the system calculates its mass. This density can be queried and set.
c++
void setDensity(float d);
float getDensity() const;
### Getting the mass
The mass of the ball can be queried, which is calculated by the function based on its radius and density.
c++
float getMass() const;
### Ball type
There are two types of balls with a given moment of inertia: a solid ball and an empty ball. You can choose between the two types with the `setType` function.
c++
void setType(BallType newType);
This function actually only sets the multiplier of the moment of inertia. This multiplier can also be queried:
c++
float getAngularMassMultiplier() const`
The multiplier can be set to any value if you do not just want to choose between the two options types.
c++
void setAngularMassMultiplier(float newAmm);
In addition, the total moment of inertia can be queried as well.
c++
float getAngularMass() const;
### Getting and adjusting the position
The position of the center of the ball can be adjusted as desired and its value can be retrieved.
c++
void setPosition(const Vec3 & p);
Vec3 getPosition() const;
### Getting and adjusting the speed
The speed of the center of the ball can be adjusted as desired and its value can be retrieved.
c++
void setVel(const Vec3 & v);
Vec3 getVel() const;
### Querying and setting the radius
The radius of the ball can be changed and its value can be queried at any time.
c++
void setRadius(float R);
float getRadius() const;
### Setting and querying the elasticity of a ball
One of the important properties of a ball is how much kinetic energy it loses during collisions. This property can also be set and queried. The higher this value, the more flexible the ball. Must be a value between 0 and 1. In the event of a collision between two balls, the two elasticities are averaged by the algorithm.
c++
void setBounciness(float k_);
float getBounciness() const;
### Coefficient of friction
Another very important property of balls is the coefficient of friction. Its value can also be set and queried. In the event of a collision between two different balls, this is also averaged for that collision.
c++
void setFrictionCoefficient(float fc_);
float getFrictionCoefficient() const;
### Update
You can use the `update` member function to update the balls. The elapsed time must be given and accordingly the function moves the ball in proportion to the speed of the ball and rotates it according to the angular velocity. You can also give the function a gravitational acceleration value to accelerate the ball in that direction.
c++
void update(float dt, const Vec3 & g = Vec3 (0, 0, 0));
### Getting a model view matrix
The `getModelViewMatrix` function can be used to generate the model view matrix that, when applied to a <mjx-container class="MathJax" jax="SVG"><svg style="vertical-align: 0;" xmlns="http://www.w3.org/2000/svg" width="1.131ex" height="1.507ex" role="img" focusable="false" viewBox="0 -666 500 666" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-3524-TEX-N-31" d="M213 578L200 573Q186 568 160 563T102 556H83V602H102Q149 604 189 617T245 641T273 663Q275 666 285 666Q294 666 302 660V361L303 61Q310 54 315 52T339 48T401 46H427V0H416Q395 3 257 3Q121 3 100 0H88V46H114Q136 46 152 46T177 47T193 50T201 52T207 57T213 61V578Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mn"><use data-c="31" xlink:href="#MJX-3524-TEX-N-31"></use></g></g></g></svg></mjx-container>-radius `SphereModel`, the geometry of the model will describe the ball. A very useful function for rendering balls.
c++
Matrix getModelViewMatrix() const;
### Speed of a given point
The `getVelInPos` member function is used to get the speed of a point on the sphere in a given position. The function includes the velocity of the center of the ball and the angular velocity of the rotation when calculating the final result vector.
c++
Vec3 getVelInPos(const Vec3 & p) const;
### Collision with a static model
Collisions with the geometry of a model are detected by the `collideWithModel` function and change the speed and angular velocity of the ball accordingly in the event of a collision. When calculating the result of a collision, the ball is considered a rigid body.
c++
void collideWithModel(const Model & m);
### Collision of two balls
The static function `collide` can collide two balls. In the event of a collision, the function removes the two balls from each other and then, as if two rigid bodies were colliding, changes their velocities and angular velocities accordingly.
c++
static void collide(Ball & b1, Ball & b2);
## The class of the scene
The class that organizes the entire application is `Scene3D`. This class handles events, handles SDL and OpenGL, runs the main loop, it contains the full application. The class declaration and implementation are contained in the `Scene3D.h` and `Scene3D.cpp` files.
c++
class Scene3D{…};
### Constructor
The constructor calls the `initWindow`, `loadGeometry` and `initShaders` functions. `initWindow` creates the window with the specified address and initializes OpenGL. `loadGeomerty` loads the geometry of the initial scene and generates the spherical model that we will draw when rendering the balls. `initShaders` compiles and links the shader program we will use for rendering. It also adjusts the position, angle, and aspect ratio of the camera and initializes the array containing the balls as an empty array.
c++
Scene3D(char const * titleStr = NULL);
### Destructor
Frees up the memory occupied by the balls and clears the shaders.
c++
~Scene3D();
### Start the main loop
By calling `enterLoop` from the `main` function, the program enters the main loop.
c++
void enterLoop();
### Saving a scene to a file
You can save a scene to a *.scene* file by calling `saveScene`. You will save the scene with the specified file name. The saved state can be reloaded at any time by drag-and-drop.
c++
void saveScene(const char * fileName) const;
### Reading and writing a scene from a stream
The scene is read from a file with an overloaded >> operator, and the `saveScene` member function also saves the scene with an overloaded << operator. The saved data: the geometry of the scene and the balls present (ball position, speed, radius, etc.).
c++
friend std::ostream& operator<<(std::ostream & os, const Scene3D & scene);
friend std::istream& operator>>(std::istream & is, Scene3D & scene);
### Functions running in the main loop
During the main loop, for the first time in each cycle, `handleEvents` queries and handles new events using SDL. The `mainLoop` member function is then called, which takes the time that has elapsed since the program was started.
c++
void mainLoop(Uint32 t = 0);
The `mainLoop` function is used to render and update balls and simulate collisions.
### Managing events
As mentioned above, events are queried and handled by the `handleEvents` function with a switch-case. For each event, it calls the appropriate event handler function.
Functions that handle each event:
* Press and release a key: use a switch case to see which key has been pressed / raised and is doing something accordingly. When escaping, releases the cursor; For WASD, space, and left shift, sets the appropriate boolean values; In case of R, it deletes the balls; T stops time; For P, saves the scene to the "saved.scene" file.
c++
void keyDownEvent(const SDLKeyboardEvent & e);
void keyUpEvent(const SDLKeyboardEvent & e);
* Move mouse: rotates the camera according to the mouse movement
c++
void mouseMotionEvent(const SDL_MouseMotionEvent & e);
* Press the mouse button: press the left button to place a new ball in the camera position
c++
void mouseButtonDownEvent(const SDL_MouseButtonEvent & e);
* Resize window: adjusts the aspect ratio of the camera and the OpenGL rendering size to the new window size
c++
void resizeEvent(int width, int height);
* Dropped file: gets the name of the dropped file and loads the new scene from it
c++
void fileDropEvent(const char * fName);
### Rendering process
Drawing consists of two main parts: drawing the world and drawing balls.
* When drawing the world, since I have decided that I do not want to shade the drawn things, in order for the appearing shapes to show their spatial shape, the program is also renders them in wireframe rendering. When rendering the world, of course, the model view matrix is an identity matrix.
* When drawing the balls, I achieved the spatial appearance with striped rendering, with the separate rendering function of `SphereModel`. The rendering is done for each ball separately, using the model view matrix queried for each ball.
Before rendering, the entire screen is colored dark gray and the Z-buffer is reset, then of course it passes the camera's perspective matrix to OpenGL.
### Placing a ball
The `placeBall` member function places a ball in place of the camera. This is called when the left mouse button is pressed.
c++
void placeBall();
Any ball can be placed with the `addBall` function. This function is used by the >> overloaded operator when the scanner reads a row containing a ball.
c++
void addBall(const Ball & b);
### Removing balls from the scene
The `clearBalls` function removes all balls from the scene. This is called when the R key is pressed.
c++
void clearBalls();
```