Gaussian beam ↩

Metadata

aliases: []
shorthands: {}
created: 2021-10-26 15:01:57
modified: 2022-01-19 16:45:35

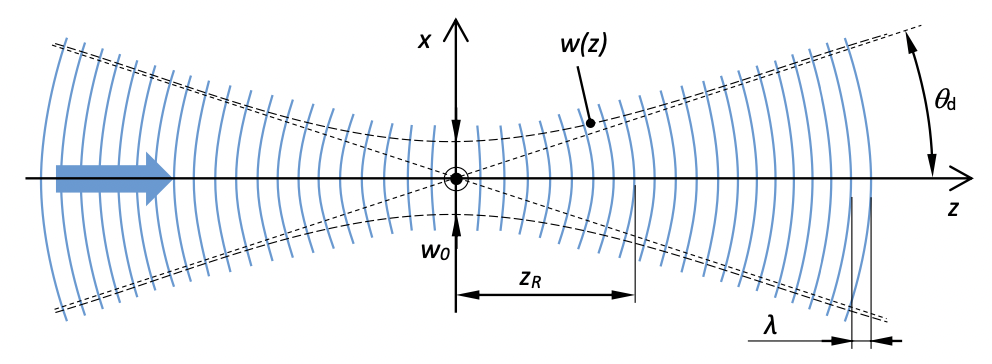
In the case of free propagation, the Gaussian beam solves the paraxial Helmholtz equation. The most simple mathematical form of a Gaussian beam that has circular symmetry around the

axis:

Where

and is the waist radius of the beam.

The evolving beam has a radius measured at the intensity:

Evolving beam radius

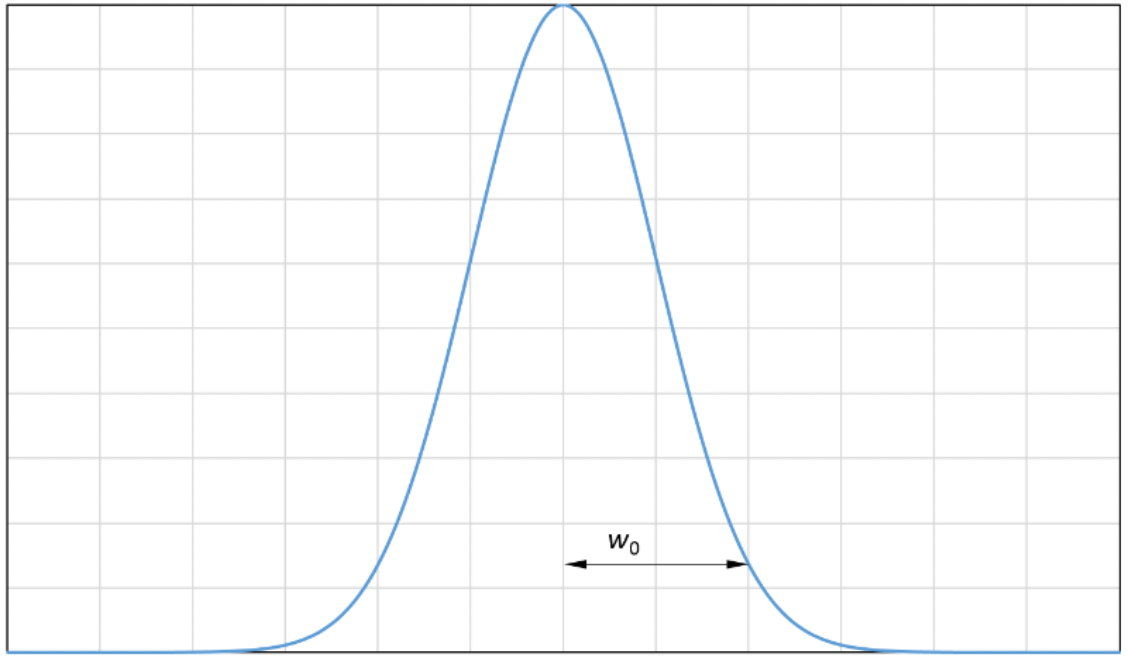
The radius of the beam increases along the axis:

Wavefront curvature

The radius of the curvature of the wavefronts of the beam:

When , then , so the beam becomes a spherical wave coming from the origin.

The curvature is zero at the waist and it is the largest at the Rayleigh distance :

The beam radius here is:

Gouy phase

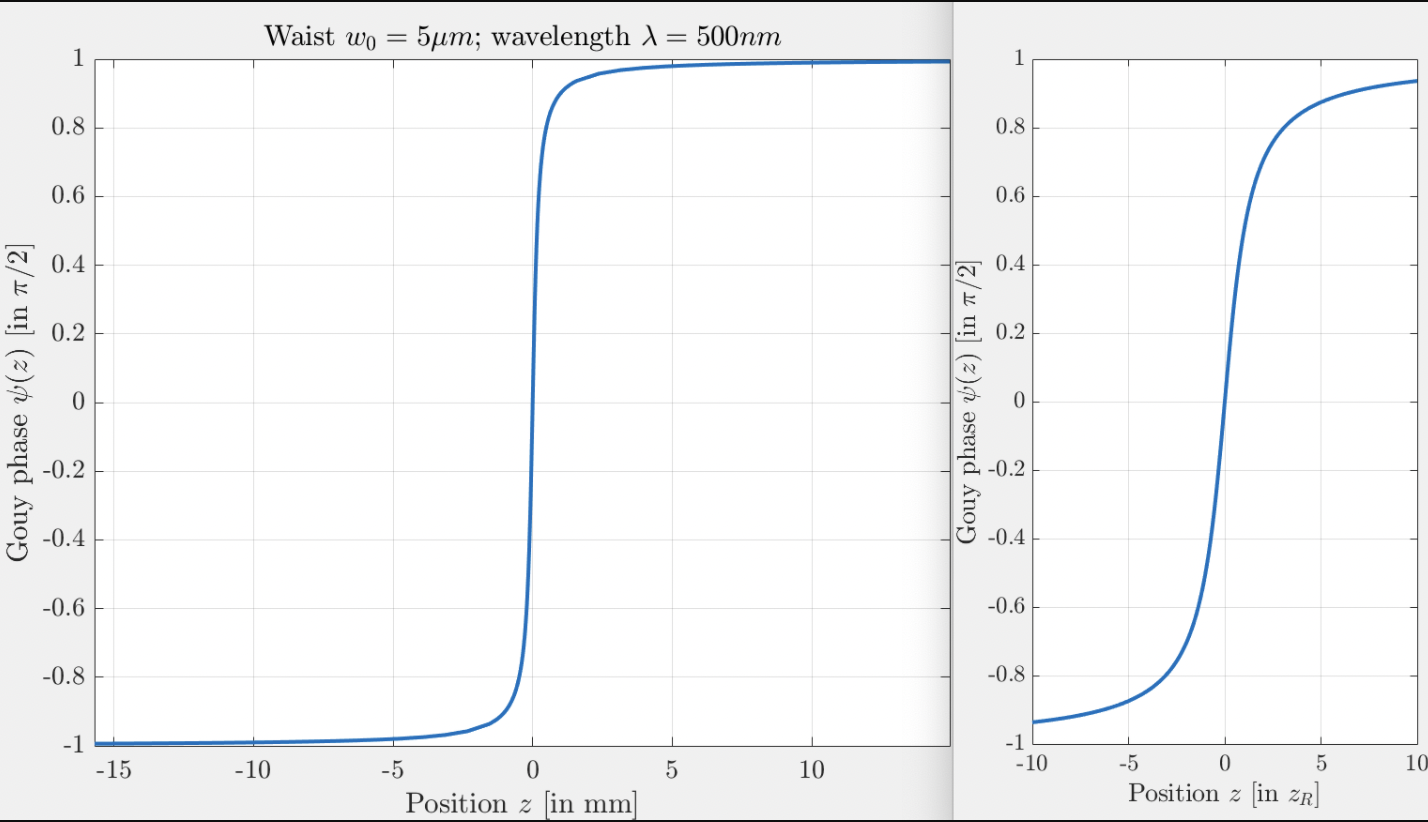
The Gouy phase advance gradually acquired by a beam around the focal region. It results in an increase in the apparent wavelength near the waist.

The relative change in the wavelength at is the following:

Example of how the Gouy phase changes along :

Divergence of the beam

When :

The Gaussian beam has the smallest divergence of any type of beam possible (it is analogous to the Gaussian wave packet in quantum mechanics, the paraxial Helmholtz equation even looks the same as the Schrödinger equation).

The condition of the Gaussian beam

Can be expressed as a relation of the waist radius and the wavelength: