Metadata
shorthands: {}
aliases: [Principle of least time]
status:
created: 2021-10-24 21:50:33
modified: 2022-01-20 18:56:07
Original form: the path taken by a ray between two given points is the path that can be traveled in the least time.
Better, "weaker" form: the path taken by a ray between two given points is the path that can be traveled in time that is stationary with respect to variations in the path. (The deviation in the path is at most a second-order change in traversal time.)
The principle works just as well when instead of time, we search for paths where the optical path length is minimized.
This principle links ray optics with wave optics.
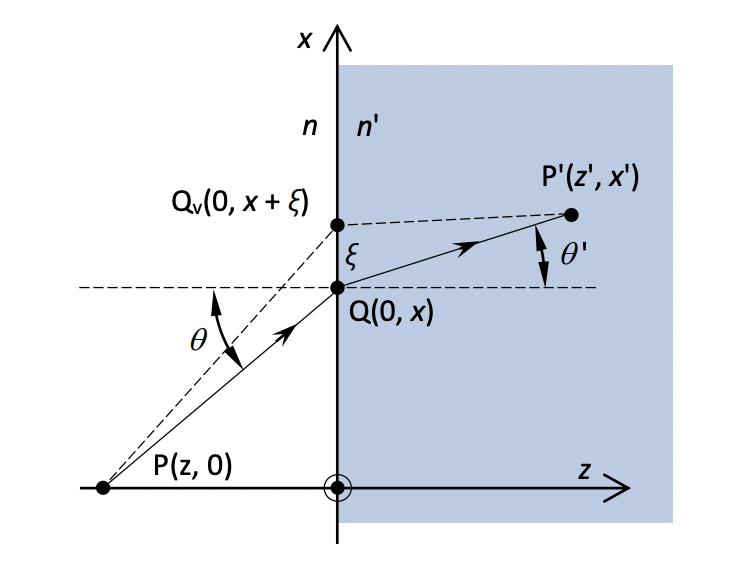
We have two media with refractive indices of

We give the path some variation by moving the
If
Then using the trigonometric relations:
Parabolic reflectors have a focal point
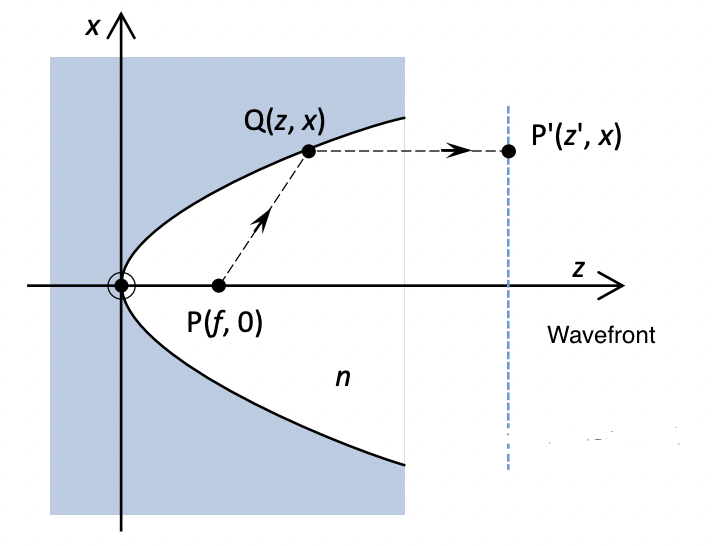
The
Now we use a strange, but useful simplification: let
If a ray goes along the
But all the other rays have the same OPL, so:
Then we can see that the reflective surface is indeed a parabola: