Cauchy sequence ↩

Metadata

aliases: []
shorthands: {}
created: 2021-12-03 00:51:48
modified: 2022-01-10 04:13:04

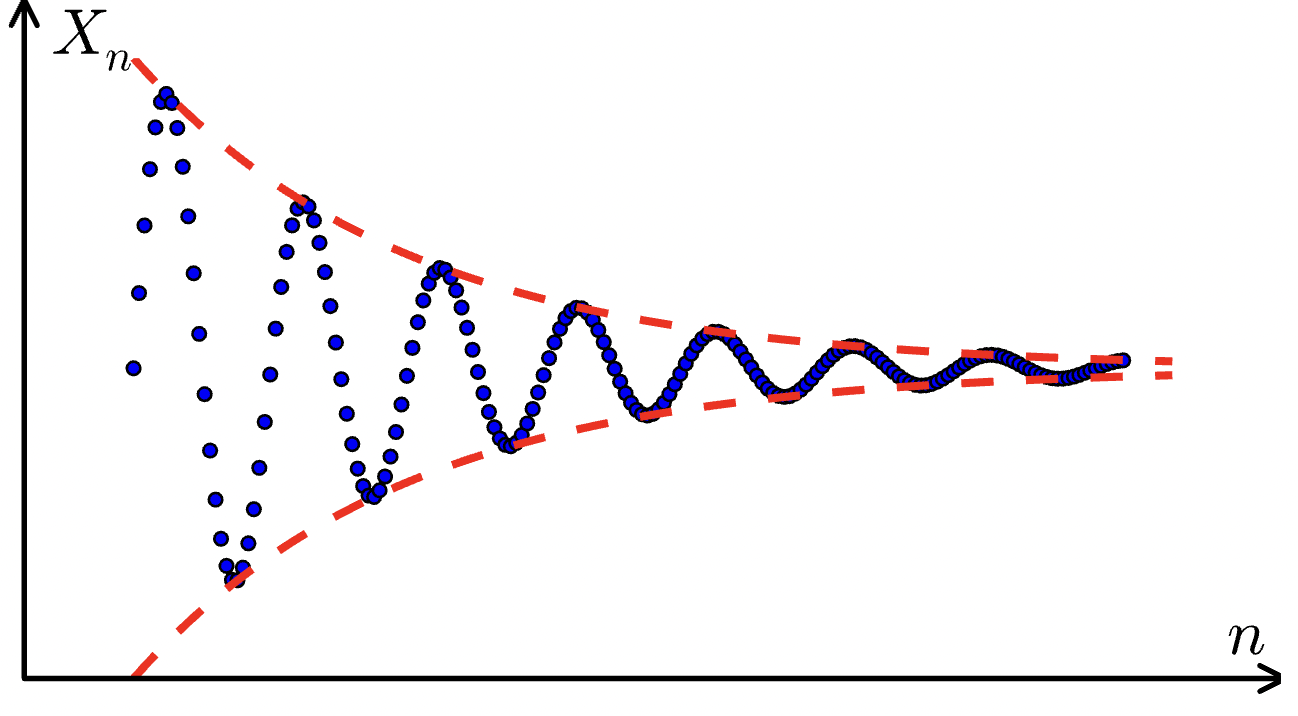
A sequence

in a metric space

is called Cauchy sequence if for every

real number, there exists a positive integer

, such that for all positive integers

This suggests that the elements of the sequence are getting closer and closer together, suggesting that the sequence might have a limit in . However this is not always the case, this limit does not always exist in . The property of a metric space that every Cauchy sequence converges in the space is called completeness